X-rays are refracted when passing areas with changing optical density. Mostly this will be when passing a boundary surface between gas or vacuum and solid or liquid matter.
Refraction is described using the complex index of refraction n*:

with n the real part, and β the imaginary part (β and n listed values e.g.) of the complex index of refraction n*. For X-rays this often is written as

with
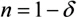
and the decrement δ. This notation is useful as for X-rays the values of δ are positive and very small (e.g. in the range of 10-4 to 10-6, see fig. 1).

Fig. 1: Decrement δ of the index of refraction n for some polymers typically used as materialfor refractive X-ray lenses
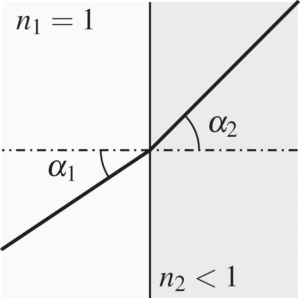
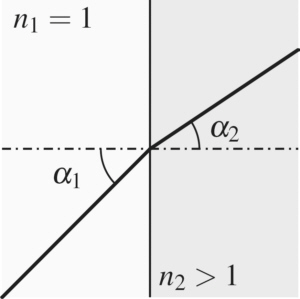
As n is smaller than one for X-rays in any matter, X-rays coming from e.g. air or vacuum and entering solids or liquids are refracted away from the normal of the refracting surface (fig. 2). For visible light, the rays are refracted towards the normal of the refracting surface. A consequence of this fact is, that refractive focussing lenses for X-rays have to be shaped like dispersing lenses for visible light, i.e. they have to be thinner in the centre than at their edge (see CRL).
 |
 |
|
| X-ray refraction | VIS refraction |
Fig. 2: Direction of refracted light for X-rays (left picture) entering from vacuum (white) into a solid or liquid (grey) and visible light (right picture); for X-rays the angle α2 is nearly the same as α1: for clarification it has been strongly exaggerated
The angles of refraction are calculated with the Snell's law (also called "Snellius' law", "Descartes' law" or "law of refraction"):
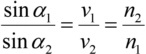
with the angles of incidence αi and the speed of light vi in the area with the index of refraction ni . The index of refraction ni is the speed of light in vacuum c0 divided by the speed of light vi in matter:
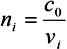
As the decrement δ of the index of refraction is small, the resulting angles of refraction are very small as well.


